09/21/17

Finished LinkedList Problem

Programming Interview Explored

Linked List

1 Design a stack:

Stack: LIFO （后入先出)，只需要存储一个 head 指针，每次的 push 和 pop 只需要针对头部的第一个元素进行。

2 Mth-to-Last element of a Linked List

双指针，第一个指针先走m步，然后第一个指针和第二个指针同时往右遍历，当第一个指针为null时，第二个指针就为倒数第m个元素

3 Null or cycle

Start slow pointer at the head of the list

Start fast pointer at second node
Tree & Graph

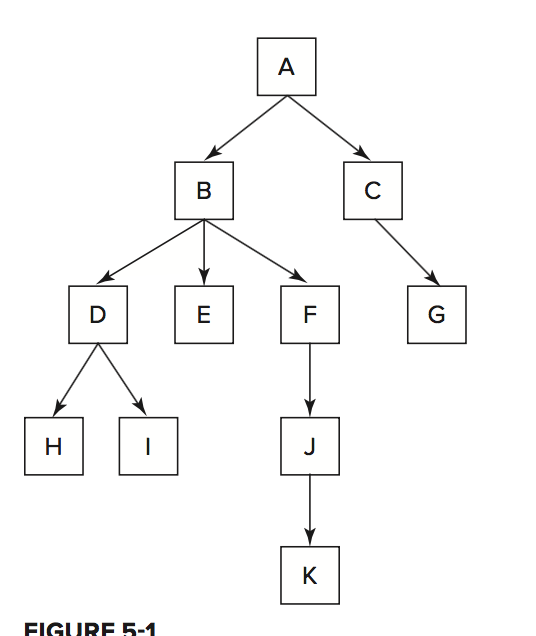
Some additional tree-related terms to know are:

Parent — Anode that points to other nodes is the parent of those nodes. Every node except the root has one parent. In Figure 5-1, B is the parent of D, E, and F.

Child — Anode is the child of any node that points to it. In Figure 5-1, each of the nodes D, E, and F is a child of B.

Descendant(后代) — All the nodes that can be reached by following a path of child nodes from a particular node are the descendant sof that node. In Figure 5-1, D, E, F, H, I, J, and K are the descendants of B.

Ancestor(祖先） — An ancestor of a node is any other node for which the node is a descendant. For example, A, B, and D are the ancestors of I.

Leaves — The leaves are nodes that do not have any children. G, H, I, and K are leaves.

BST

Here’s an implementation of the search in C# or Java:

Node findNode( Node root, int value ){ 
    while( root != null ){
    int currval = root.getValue(); 
    if( currval == value ) break; 
    if( currval < value ){
root } 
    else { root
} 
    }
return root; 
    }

For example, log28 = 3 because 2^3= 8, so the running time of the lookup operation isO(log2(n)). Because logarithms with different bases differ only by a constant factor, it’s common to omit the base 2 and call thisO(log(n)). log(n) is very fast. For an example, log2(1,000,000,000) = 30.

Without ordering, the time to find a node is O(n).

Traversals

Preorder: root, left, right

Inorder: left, root, right

Postorder: left, right, root

Graphs

vertices, edges

A graph with one-way edges is called a directed graph.

A graph with only two-way pointers is called an undirected graph.

Graphs can be present as adjacency(临近) list or adjacency matrix.

Height of a Tree

The height of a tree equals the height of its tallest subtree plus one.

int treeHight (Node n) {
    if (n == NULL) return 0;
    return 1 + max(treeHight(n->left), treeHight(n->right) );
    }

Preorder Non recursion

C
reate the stack

Push the root node on the stack

While the stack is not empty

Pop a node

Print its value

If right child exists, push the node's right child

If left child exists, push the node's left child

The code (with no error checking) for this algorithm is as follows:

void preorderTraversal( Node root ){
 NodeStack stack = new NodeStack();
 stack.push( root );
 while( stack.size() > 0 ){
 Node curr = stack.pop();
 curr.printValue();
 Node n = curr.getRight();
 if( n != null ) stack.push( n );
 n = curr.getLeft();
 if( n != null ) stack.push( n );
 }
}

Lowest Common Ancestor

E
xamine the current node

If value1 and value2 are both less than the current node's value

Examine the left child

If value1 and value2 are both greater than the current node's value

Examine the right child

Otherwise
, The current node is the lowest common ancestor

This solution may seem to suggest using recursion because it is a tree and the algorithm has a

recursive structure to it, but recursion is not necessary here. Recursion is most useful when moving

through multiple branches of a tree or examining some special pattern of nodes. Here you are only

traveling down the tree. It’s easy to implement this kind of search iteratively:

Node findLowestCommonAncestor( Node root, int value1, int value2 ){
 while( root != null ){
 int value = root.getValue();

 if( value > value1 && value > value2 ){
 root = root.getLeft();
 } else if( value < value1 && value < value2 ){
 root = root.getRight();
 } else {
 return root;
 }
 }
 return null; // only if empty tree
}

9/22

Binary tree min path,

Check if graph is cycle,

increasing array